OVERVIEW
A swing chart is another member of a genre of charts referred to as reversal charts. As stated in Chapter 7, a reversal chart is any chart that filters raw data in order to accentuate significant points of interest while ignoring points of less interest. All technical analysts find peaks and valleys of great interest, whereas they find areas of lateral price movements less interesting. Peaks and valleys are those points of inflection where price directions reverse and the slope of an existing trend changes its arithmetic sign (minus to plus and plus to minus) (Figure 9-1).
A swing chart is another member of a genre of charts referred to as reversal charts. As stated in Chapter 7, a reversal chart is any chart that filters raw data in order to accentuate significant points of interest while ignoring points of less interest. All technical analysts find peaks and valleys of great interest, whereas they find areas of lateral price movements less interesting. Peaks and valleys are those points of inflection where price directions reverse and the slope of an existing trend changes its arithmetic sign (minus to plus and plus to minus) (Figure 9-1).
DEFINITIONS
In this book, we prefer to use the original terms of trader/theoretician R. N. Elliott to avoid any unnecessary confusion with terms used by other swing analysts.
In this book, we prefer to use the original terms of trader/theoretician R. N. Elliott to avoid any unnecessary confusion with terms used by other swing analysts.
- A wave is a single straight line in a swing chart. Waves are always diagonal lines with positive or negative slope, never perfectly horizontal or vertical.
- A peak is the point of intersection between an upward wave on the left and a downward wave on the right. This represents a local maximum in the raw data.
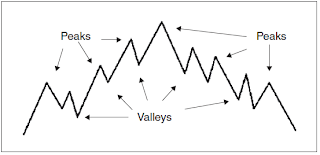 |
| Figure 9-1 Peaks and Valleys. |
- A valley (or trough) is the point of intersection between a downward wave on the left and an upward wave on the right. This represents a local minimum in the raw data.
- A cycle is a series of adjacent interconnected waves depicting specific price formations.
To convert a sequence of raw tick data or OHLC interval data to swing data, a swing-reversal algorithm is employed in which two user-supplied variables must be initialized, the minimum fluctuation unit and the minimum reversal amount.
MINIMUM FLUCTUATION UNIT
Traditionally, the minimum price unit is the smallest fractional price increment that a quote currency (or underlying security) can change. This is very similar to box size in point and figure charting. In the currency markets, this increment is a single pip. For example, if the EURUSD currency pair is currently trading at 1.2451, a single pip is 0.0001 USD.
Traditionally, the minimum price unit is the smallest fractional price increment that a quote currency (or underlying security) can change. This is very similar to box size in point and figure charting. In the currency markets, this increment is a single pip. For example, if the EURUSD currency pair is currently trading at 1.2451, a single pip is 0.0001 USD.
There are three cases where a minimum fluctuation unit greater than 1 pip might be used. One such case is when the parity rate between two currencies is very wide and causes a very large bid/ask spread. For example, if the bid/ask spread (transaction cost) for the EURCZK currency pair is 350 koruny, then a 1-pip box size will have very negligible filtering power.
A second reason for using a box size greater than 1 pip occurs when performing historical analysis and a longer time frame is being analyzed. In this case, the analyst probably will be scrutinizing major reversals and may have little interest in minor reversals. This pertains more to long-term position traders rather than to session or day traders.
Lastly, a larger box size may be used to align peaks and valleys with the grid lines of the chart. This is purely a display preference, though.
MINIMUM REVERSAL AMOUNT
The reversal amount is the number of minimum fluctuation units necessary to plot a reversal in price direction. For instance, if the current trend is upward, and the reversal amount is set at three units, then a decline of three fluctuation units must be reached before the downward movement is plotted. If, instead, a new price continues in the same direction as the existing trend, then single boxes are added automatically to the last extreme (either a peak or a valley).
The reversal amount is the number of minimum fluctuation units necessary to plot a reversal in price direction. For instance, if the current trend is upward, and the reversal amount is set at three units, then a decline of three fluctuation units must be reached before the downward movement is plotted. If, instead, a new price continues in the same direction as the existing trend, then single boxes are added automatically to the last extreme (either a peak or a valley).
It is the interaction between the minimum fluctuation unit and the reversal amount that triggers the reversal mechanism in the swing algorithm necessary to plot peaks and valleys while ignoring lateral price movements.
There is one final case for increasing the minimum fluctuation unit. If an analyst, for whatever reasons, has become very partial to one specific reversal amount, it is possible to increase the minimum fluctuation unit instead of the reversal amount when market conditions change.
For example, a three-unit reversal amount is favored by many traders. If traders wish to filter out some of the minor swings, they can increase either the reversal amount or the minimum fluctuation unit. However, keep in mind that although an algorithm with a 2-pip unit size and a three-unit reversal amount will generate results very similar to an algorithm with a 1-pip unit size and a six-unit reversal amount, they will not be identical. This requires some reflection. The reason is that when you plot a continuation of an existing trend, smaller distances can be plotted.
SWING-REVERSAL ALGORITHM
Given the information and user-supplied variables generated earlier, we will now define the swing-reversal algorithm as follows (this algorithm assumes that we are using daily OHLC quotes as the input data rather than simply the closing prices):
Given the information and user-supplied variables generated earlier, we will now define the swing-reversal algorithm as follows (this algorithm assumes that we are using daily OHLC quotes as the input data rather than simply the closing prices):
Step 1: Initialize BoxSize and ReversalAmount variables.
Step 2: Create a new variable called Direction.
Step 3: Create two array variables called Price and Time to hold the swing data.
Step 4: Set Price(1) Close(1) and Time(1) 1.
Step 5: If High(2) – Price(1) BoxSize *ReversalAmount, thenSet Price(2) High(2).
Set Time(2) 2.
Set Direction UP.ElseIf Price(1) – Low(2) BoxSize *
ReversalAmount, thenSet Price(2) Low(2).
Set Time(2) 2.
Set Direction DOWN.ElseIncrement day number and repeat step 5End IfStep 6: Increment DayNo.If DayNo Number of OHLC quotes, thenGo to step 9.If Direction DOWN, thenGo to step 8.End IfStep 7: If High(DayNo) – Price(Idx) BoxSize, thenSet Price(Idx) High(DayNo).
Set Time(Idx) DayNo.ElseIf Price(Idx) – Low(DayNo) BoxSize *
ReversalAmount, thenIncrement Swing Idx.End If
Set Price(Idx) Low(DayNo).
Set Time(Idx) DayNo.
Set Direction DOWN.Go to step 6.Step 8: If High(DayNo) – Price(Idx) BoxSize *ReversalAmount, thenIncrement Swing Idx.
Set Price(Idx) High(DayNo).
Set Time(Idx) DayNo.Set Direction UP.ElseIf Price(Idx) – Low(DayNo) BoxSize,
thenSet Price(Idx) Low(DayNo).
Set Time(Idx) DayNo.End If
Go to step 6.Step 9: Set Number of Swings Swing Idx.Exit
At this point, the two swing arrays Price(·) and Time(·) have been populated with corresponding pairs of swing data.
TIME ALIGNMENT
Adherents of the point and figure charting method believe that the compression of time along the x axis is an advantage because the trader can focus solely on price movements. Proponents of swing charts, on the other hand, are more comfortable viewing the points of inflection (peaks and valleys) as they occur in real time. When a swing chart is displayed directly below an OHLC bar chart, the respective peaks and valleys will align vertically with the corresponding bar above. Swing charts also display the velocity of the market; that is, the slope of each wave determines how quickly the market is moving.
Adherents of the point and figure charting method believe that the compression of time along the x axis is an advantage because the trader can focus solely on price movements. Proponents of swing charts, on the other hand, are more comfortable viewing the points of inflection (peaks and valleys) as they occur in real time. When a swing chart is displayed directly below an OHLC bar chart, the respective peaks and valleys will align vertically with the corresponding bar above. Swing charts also display the velocity of the market; that is, the slope of each wave determines how quickly the market is moving.
The point and figure chart versus swing chart debate is, in the final analysis, a matter of preference. Any swing chart can be readily “massaged” into a point and figure chart simply by converting the straight lines to columns of X’s and O’s. The converse, however, is not true because point and figure charts normally do not record the day numbers at the reversal vertices. We prefer the swing chart because in later chapters the number of time units in each wave will be used in numerous mathematical calculations.
PRACTICAL EXAMPLES
In the swing charts in Figures 9-2 through 9-5, the minimum fluctuation unit is set to 1 pip, whereas four different reversal amounts (3, 6, 9, and 12) are employed.
In the swing charts in Figures 9-2 through 9-5, the minimum fluctuation unit is set to 1 pip, whereas four different reversal amounts (3, 6, 9, and 12) are employed.
 |
| Figure 9-2 Three-box Reversal. |
 |
| Figure 9-3 Six-box Reversal. |
 |
| Figure 9-4 Nine-box Reversal. |
 |
| Figure 9-5 Twelve-box Reversal. |
 |
| Figure 9-6 Composite Swing Chart. |
As stated earlier, the number of waves generated by the swing algorithm has an inverse relationship with the reversal amount, i.e., as the reversal amount increases, the number of waves decreases, and vice versa (Table Inverse Relationship). Using the EURUSD currency pair for the time frame specified earlier, this equates to
 |
| Inverse Relationship |
COMPOSITE SWING CHARTS
Figure 9-6, an aggregate of the preceding four swing charts, is included here so that traders can conceptually scrutinize the effect of different reversal amounts when using the same OHLC data.
Figure 9-6, an aggregate of the preceding four swing charts, is included here so that traders can conceptually scrutinize the effect of different reversal amounts when using the same OHLC data.
USAGE
The advantages of comparing identical raw data time frames using different reversal amounts are twofold. First, any time traders view a single data set from different perspectives, there is a greater likelihood of discovering one particular nuance in one of the charts that may not be readily apparent in the sibling charts (more is better). Additionally, several trading systems are based on specific swing patterns, such as Elliott cycles and other patterns discussed later in this book. Some of these systems generate a discrete price estimate or at least predict price direction. Systematically varying the reversal amount allows traders to compare and log the forecasts at different levels, which adds an additional tier of reliability in the signal confirmation mechanism.
The advantages of comparing identical raw data time frames using different reversal amounts are twofold. First, any time traders view a single data set from different perspectives, there is a greater likelihood of discovering one particular nuance in one of the charts that may not be readily apparent in the sibling charts (more is better). Additionally, several trading systems are based on specific swing patterns, such as Elliott cycles and other patterns discussed later in this book. Some of these systems generate a discrete price estimate or at least predict price direction. Systematically varying the reversal amount allows traders to compare and log the forecasts at different levels, which adds an additional tier of reliability in the signal confirmation mechanism.